In addition to TDAP with atomic orbital basis[1-3], we also implement the TDDFT approach in the Quantum Espresso using plane waves (PW) basis \(\{ \mathbf{G} \}\). In the PW basis, the time-dependent Kohn-Sham (TDKS) state \(\psi_{\gamma \mathbf{k} }( \mathbf{G},t)\) is governed by the TDKS equation at each \(\mathbf{k}\) point in the Brillouin zone[4]: 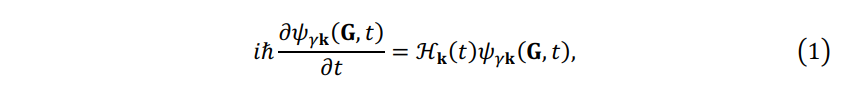where, \(\gamma = 1, N_e\) denotes TDKS state index, and \(N_e\) is the number of electrons. \(\mathcal{H}_\mathbf{k}(t)\) is the Hamiltonian operator represented in the PW basis, which element is 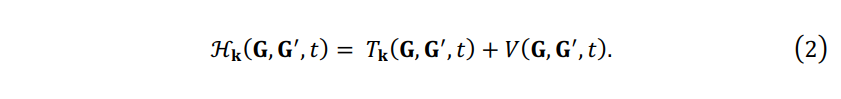\(\mathbf{T}_\mathbf{k}( \mathbf{G}, \mathbf{G}^{'} )\) is the kinetic energy operator, 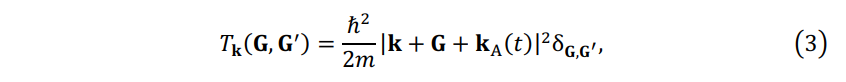where \(\mathbf{k}_A(t)\), the vector potential, is the integral of electric field \(\mathbf{E}\) [5, 6], 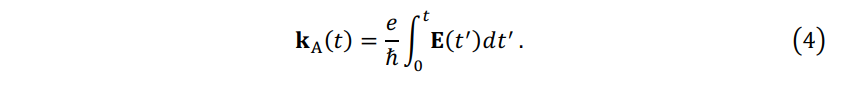The potential operator, \(V( \mathbf{G}, \mathbf{G}^{'} )\), is the function of charge density \(\rho(t)\).