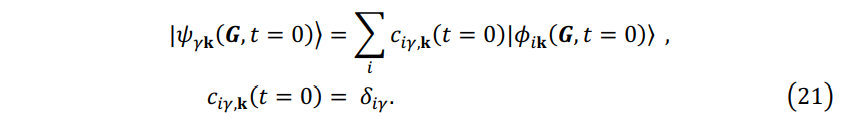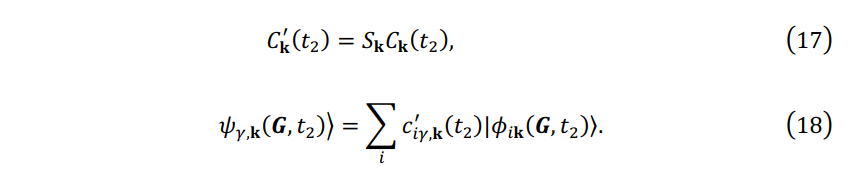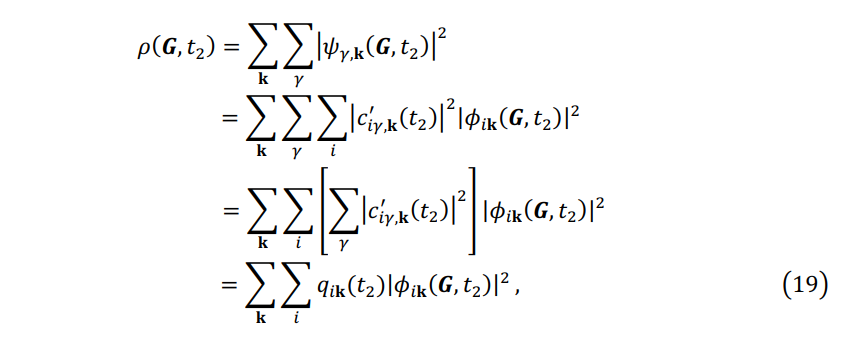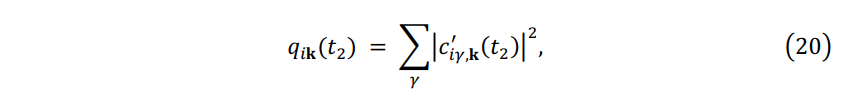In order to calculate charge density \(\rho(t_2 )\), we change the basis from \(\{ \phi_{i\mathbf{k}}(\mathbf{G},t_1) \}\) to \(\{ \phi_{i\mathbf{k}}(\mathbf{G},t_2) \}\) , Charge density \(\rho(t_2 )\) can be calculated with \(c_{i\gamma,\mathbf{k}}^{'}(t_2)\) and \(\phi_{i\mathbf{k}} (\mathbf{G},t_2 )\) as: where is the population of the adiabatic states.

In fact, Equation 19 ignores the cross term \(c'^*_{i\gamma,\mathbf{k} }c'_{j\gamma,\mathbf{k} }\phi^*_{i\gamma,\mathbf{k} }(\mathbf{G} ,t_2)\phi_{j\gamma,\mathbf{k} }(\mathbf{G} ,t_2)\) for \(i \ne j\).
Set rho_debug = .True.(TDAPW-6.4) or use_tdks = .True.(TDAPW-6.6), Charge density \(\rho(t_2 )\) is calculated by

\[\rho(\mathbf{r},t_2) = \sum_k \sum_\gamma \psi^*_{\gamma,k}(\mathbf{r},t_2) \psi_{\gamma,k}(\mathbf{r},t_2)\]

         The initial state of TDKS orbital is the ground state of DFT calculated by Quantum Espresso,